Who Discovered the Quadratic Formula

This is the quadratic formula:  x_1,2=(-b/2a) ± (1/2a)(b²-4ac)^1/2

It is said the quadratic formula has been used and known by man for thousands of years. The equation has changed a number of times, too.

Some 2000 years ago, the Chinese, Babylonians, and Egyptians already knew the area of a square  levels with the length of its sides. Using bales of hay, they figured they could stack nine bales more if the roof space were three times wider.  The Chinese, Babylonians, and Egyptians could compute the area of other complex shapes.

But they did not know how to work out the sides of those shapes. And so they were faced with a bigger problem: They had to be able to calculate the length of the sides starting from a certain point. The shape should be leveled with a total area using the lengths of the sides.

 

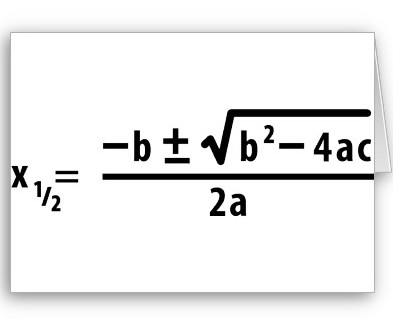
How the Egyptians used the quadratic formula

1, 500 years ago, the Egyptians did not use numbers like we do today. They expressed mathematical problems using words. But Egyptian scribes skirted the quadratic equation issue by solving the area of all sides and made a reference chart. They made up something like a multiplication table.  That made computation fast and quick. Egyptian engineers did have to compute all shapes and sides all the time. All they had to do was look at the chart.

Up this day these tables till exist. They may not be mathematically correct, but they certainly show how the quadratic formula began.   .

 

How the Babylonians used the quadratic formula

The Babylonians had a different way of solving the problem. Unlike the Egyptians, the Babylonians used numbers instead of words. The Babylonians numbers were pretty much the same as the numbers we use today, except that theirs were based on a hexagesimal model (or base 60). With this system multiplication and addition were easier to do. So around 1000 BC Babylonian engineers could check whether the values of their tables were right or wrong.  The Babylonians came up with a technique called “completing the square” to solve common problems with areas by 400 BC.

 

 

 

Euclid and Pythagoras

The first purely mathematical try to come up with a quadratic formula was done by Pythagoras in 500 BC. Euclid did the same thing in Alexandria, Egypt. Euclid used a purely geometric method. And he came up with a general formula to solve the equation. For his part Pythagoras observed that the ratios between the area of a square and the length of the sides did not add up. To him there was no other proportion except the rational. Euclid thought otherwise: If there are rational numbers, there must be irrational numbers.  He then wrote a book called Elements in which he lay down the mathematics of solving quadratic equation.

But Euclid’s equation did not use the same formula that we know today. His formula could not compute the square root of any number by longhand.

How Hindu mathematicians added 0 to the equation

The Hindus are credited to have created the concept of 0, for nothingness. Western mathematicians could bring themselves to believe in the value of nothing. The Hindus, on the other hand, believed in “shunya” , meaning the void, or a state of equilibrium.

By 700 AD, a Hindu mathematician named Brahmagupta was using irrational numbers. He came up with two roots in the answer. But around 1100 AD,  another Hindu math wizard, Baskhara, discovered that any positive number has two square roots.

 

How the quadratic equation spread to Europe

Mohammad bin Al-Khwarismi, a respected Muslim mathematician in Baghdad was able to solve the quadratic equation in 820 AD. He did not use numbers nor negative solutions. Word got around about what he did. So a Jewish mathematician named Abraham bar Hiyya brought this piece of knowledge to Barcelona, Spain in 1100.

From then on mathematicians all over Europe picked up and used the equation.